Механіка
Елементи СТВ
Молекулярна фізика та термодинаміка
Електродинаміка
- Електричне поле
- Постійний електричний струм
- Електричний струм в різних середовищах
- Магнітне поле
- Електромагнітна індукція
Електромагнітні коливання і хвилі
Оптика
Атомна та ядерна фізика
1.1. ОСНОВНА ЗАДАЧА МЕХАНІКИ. ОСНОВНІ ПОНЯТТЯ КІНЕМАТИКИ
1.2. РІВНОМІРНИЙ ПРЯМОЛІНІЙНИЙ РУХ. ШВИДКІСТЬ РУХУ
1.3. РІВНОПРИСКОРЕНИЙ ПРЯМОЛІНІЙНИЙ РУХ. ПРИСКОРЕННЯ
1.4. ВІЛЬНЕ ПАДІННЯ ТІЛ
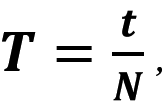
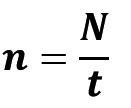
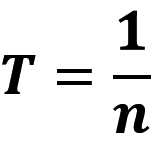
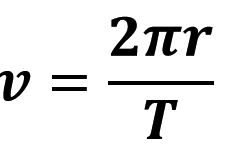
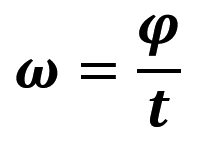
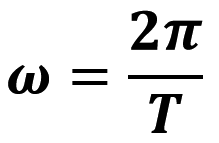
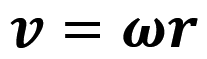
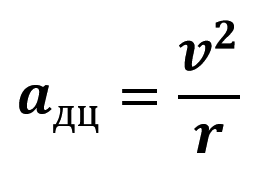
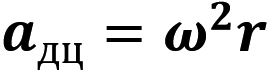
1.5. РІВНОМІРНИЙ РУХ МАТЕРІАЛЬНОЇ ТОЧКИ ПО КОЛУ
Рівномірний рух тіла по колу — це такий криволінійний рух, за якого траєкторією руху тіла є коло, а лінійна швидкість руху не змінюється з часом.
Період обертання Т – фізична величина, що дорівнює інтервалу часу, за який тіло здійснює один оберт:
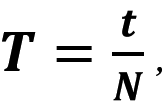
де N – кількість обертів, здійснених тілом за інтервал часу t.
Одиниця періоду обертання в СІ – секунда: [T] = 1 с.
Обертова частота n – фізична величина, яка чисельно дорівнює кількості обертів за одиницю часу:
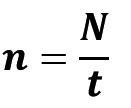
Одиниця обертової частоти в СІ – оберт за секунду: [n]= 1 с-1
Період і обертова частота є взаємно оберненими величинами:
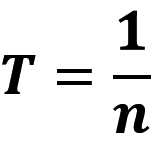
За періодом обертання T та радіусом колової траєкторії r легко визначити лінійну швидкість v рівномірного руху тіла по колу:
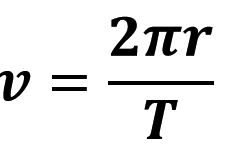
Кутова швидкість – це фізична величина, яка чисельно дорівнює куту повороту радіуса за одиницю часу:
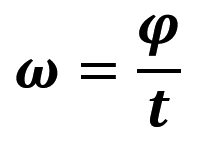
де ω – кутова швидкість;
φ – кут повороту радіуса за інтервал часу t.
Одиниця кутової швидкості в СІ – радіан за секунду: [ω] = 1 рад/с.
За час, що дорівнює одному періоду (t=T), радіус виконує один оберт (φ=2π), тому кутову швидкість можна обчислити за формулою:
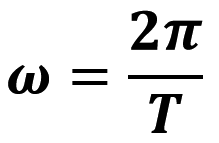
Кутова і лінійна швидкості пов’язані співвідношенням:
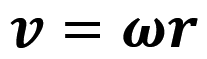

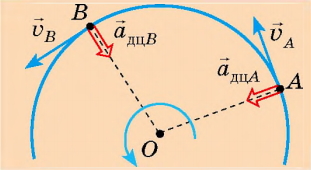
У разі рівномірного руху тіла по колу вектор прискорення напрямлений до центра кола – саме тому прискорення рівномірного руху тіла по колу називають доцентровим прискоренням адц.
Модуль доцентрового прискорення обчислюють за формулами:
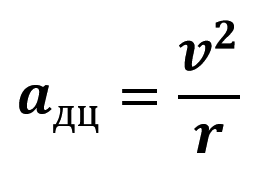
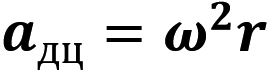
де v — лінійна швидкість; r — радіус кола; ω — кутова швидкість.

